本文翻译节选自我的一个笔记,为了偷懒,一些定义和证明就保持原样了。
染色问题最著名的理论是拉姆齐理论,它描述的是对有限整数集合或者所有自然数的任意染色下局部拥有的单色性。这一定理可以推广到可数甚至与一些大基数(large cardinals)。关于无限的拉姆齐理论可以参考这个 Notes。至于满足单色性的局部性质,拉姆齐定理并没有给出这些性质的具体形式。然而, Van der Waerden 定理和 Hales–Jewett 定理等结论给出了一些具体的形式,比如前者是等差数列总有单色解,后者更是前者的推广。另一个有意思的局部性质是“单色方程解”,满足这一特性的方程我们称为“分割正规的”(partition regular)。
Definition 1. An equation $f(x,y,z,\dots)=0$ is partition regular (or simply regular) if, and only if, for any finite partition of $\mathbb{N}$ into $C_1, C_1,\dots, C_r$, there exists some $C_i$ containing a non-trivial solution to the equation.
Schur 最早研究了分割正规的Schur方程,也就是最简单的线性齐次方程 $x+y=z$。Schur定理表明,对自然数的任意有限染色,上述方程都有单色解。为了更好的理解,我们考虑二染色,用反证法可以证明在二染色情况下,总存在单色解。
实际上,对于二染色的情况,我们只需要考察前5个数即可。不妨假设1被染成蓝色,因为 1+1=2 ,所以2只能被染成红色,同理4只能被染为蓝色。而1+3=4则表明 3 只能被染为红色。因此 ${1,2,3,4}$ 被唯一(不考虑特定颜色)分割为两个单色子集 ${1,4}$ 和 ${2,3}$ 。而 5=2+3=1+4 导致必然有一个单色解(5要么是蓝色要么是红色)。在这一情况下,我们称 5 为方程 x+y=z 的 Schur 数 $S(2)$ 。上述“证明”也表明Schur方程是 2-regular 的。更一般地,对任意的方程或者方程组,我们定义 Rado 数如下:
Definition 2. Given an equation or a system of equations $\mathcal{L}$ and finite $r$ colors, the Rado number $R(\mathcal{L},r)$ is the least number such that any $r$-coloring of ${1,2,\dots,R(\mathcal{L},r)}$ must contain a monochromatic solution to $\mathcal{ L}$.
对于一般的线性齐次方程 $a_1 x_1+\cdots+a_nx_n=0$ , Schur 的学生 Rado 给出了线性齐次方程是否是分割正规的充分必要条件:
Theorem 3 (Rado’s Theorem [1]). A linear homogeneous equation $a_1 x_1+\cdots+a_nx_n=0$ is partition regular on $\mathbb{N}$ if and only if there exists a nonempty set $J\subseteq{1,\dots,n}$ such that $\sum_{j\in J}a_j=0$.
上述定理也有乘积形式的非线性方程的定理。对于不是分割正规的方程,我们也会考察一个弱化的条件,即上文提到的 r-regular,r 染色的分割正规性。进一步地,我们有正规次数的定义
Definition 4. The degree of regularity of an equation or a system of equations $\mathcal{L}$ is the largest integer $r\geq 0$, if any, such that $\mathcal{L}$ is $r$-regular. This number is denoted by $\mathrm{dor}(\mathcal{L})$. In particular, if $\mathrm{dor}(\mathcal{L})=\infty$, then $\mathcal{L}$ is regular.
让我们回到 Schur 方程,我们可以手工计算得到 $S(3)=14$。Golomb 和 Baumert [2] 证明了 $S(4)=45$。至于 S(5),悬而未决了多年,直到最近,Heule [3] 才使用计算机方法 SAT solver 证明了 $S(5)=161$。而 $S(r);(r\geq6)$ 到目前为止还是未解的。
在方程的正规性这一领域中的最著名的问题是 Erdos 和 Graham 提出的勾股方程的正规性,这一问题目前仍然是未解的,甚至对于特定的 r, r-正规性也长期没有任何突破。直到2016年,Heule, Kullmann 和 Marik [4] 使用 SAT solver 反向树的方法证明了 $$ R(x^2+y^2=z^2,2)=7825 $$ 这一证明被称为“世界上最长的证明”,有 200 TB 证明数据。当时有大量媒体报道这一证明,其中每日邮报当时报道的标题是:“World’s longest maths proof: Solution to a 30-year-old problem would take 10 BILLION years to read—all for a prize of just $100.”但实际上,他们还不能获得这一100美元奖金。因为悬赏100美元的问题是完整解决勾股方程的正规性,而他们的工作仅仅只是解决这一问题的一小步。
而在方程正规性的理论证明中,Nasso 和 Baglini [5] 给出了最好的结果。他们给出了一系列满足分割正规性的方程的充分条件和必要条件。比如,他们证明了扩展的Rado多项式:
$$ R(x_1,\dots,x_n,y_1,\dots,y_k)=c_1x_1+\cdots+c_nx_n+P(y_1,\dots,y_k) $$ (n≥2,P是没有常数项的整系数多项式)在N上是正规的当且仅当存在非空子集 $J\subseteq {1,\dots,n}$ 使得 $\sum_{j\in J}c_j=0$。不仅仅如此,诸如 $x_1x_2=y_1y_2+z^2$ 等大量方程也能被证明是正规的。
不幸的是,Nasso 和 Baglini 的理论还是无法判断勾股方程的分割正规性。它是2-正规的依然是目前我们知道的最好的结果。
不过让我们来看一些其他的例子,比如 $x+y=z^2$ 。根据Nasso 和 Baglini 的理论,这一方程不是正规的。但是对于不正规的方程我们乐于考察他们的正规次数。 Lindqvist [6] 最近证明了它的正规次数是2, 即它是2-正规但不是3-正规的。需要注意的是,这一方程有一个平凡解(x=y=z=2),我们讨论的单色解都排除这样的情况。Lindqvist 对于这一方程的非3-正规的构造性证明仅有十几行,而对2-正规(更严格地说,他证明了2-强正规,即对任意有限染色有无穷多对单色解)的证明则用到了解析数论等多种工具,花了近30多页。
实际上,仅仅是考察2-正规性,我们也可以通过穷举得到 $$ R(x+y=z^2,2)=32 $$ 并且能构造31以内自然数的一个无同色解的分割:
$$ C_R={1,4,5,6,7};\\ C_B={2,3,8,9,10,11,12,15,18,19,20,21,24,29,30,31}. $$
让我们用上述方法讨论一下如下方程: $x+y=2z^2$ 。这一方程同样不是正规的,且是非3-正规,我们通过略微修改Lindqvist的证明既可证明非3-正规性。
证明. We color all the points in each dyadic block $A_i={n\in \mathbb{N}:2^i\leq n <2^{i+1}},$ $i=0,1,2,\dots$, in one color $c_i$. We assign $c_0,c_1,c_2$ to be different and let $c_i\notin{c_{\lfloor{i/2}\rfloor-1},c_{\lfloor {i/2}\rfloor}}$, for all $i\geq 3$. This is possible, since $\lfloor{i/2}\rfloor\leq i$ for all $i\geq 3$ (actually for all $i\geq 0$). Without loss of generality, suppose $x\leq y, y\in A_i$, then we have $2^i<x+y< 2^{i+2}$, hence $2^{(i-1)/2}<z<2^{(i+1)/2}$. Since $\frac{i-1}{2}\geq \lfloor\frac{i}{2}\rfloor-1$ and $(i+1)/2\leq \lfloor\frac{i}{2}\rfloor+1$, it follows that $z\in A_{\lfloor{i/2}\rfloor-1}\cup A_{\lfloor{i/2}\rfloor}$. By construction, the only way that such a $z$ can have the same color as $y$ is if $i \in {0,1,2}$, in which case $x\leq y<8$, and so $z=1$ or $2$. If $z=1$, then this is the trivial solution $x=y=z=1$. If $z=2$, then $x+y=8=2\cdot 2^2$. Here are all the possible options {1,7,2}, {2,6,2}, {3,5,2} and {4,4,2}. It is easy to check that there is no monochromatic solution in those options.
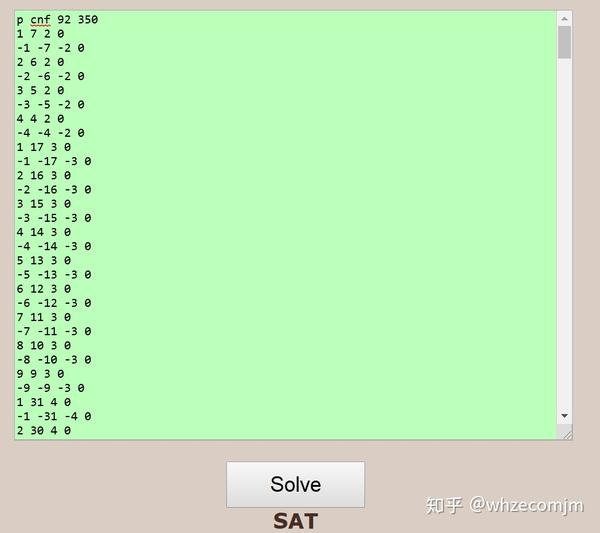
接下来我们可以使用穷举法考察 2-正规性。然而过程没有那么顺利,通过简单的枚举我们可以得到有如下的同色子集 ${3,4,5,6}$。于是我试图使用 SAT solver。SAT solver 是一个“逻辑计算器”,我们需要把我们的问题(在正规性检测中我们需要输入反问题)转化为合取范式的问题才能放入 SAT solver。感兴趣的可以去了解一下 SAT,这里就不详述了。虽然有很多现成的 SAT solver,但是为了方便我还是找到了一个现成的在线的 SAT solver SAT.js. 由于不知道这一问题的 Rado 数的大小,我先尝试了 100。结果发现,仅仅当z≤9时,我们就能得出矛盾,也就是说 Rado数必然比100小。用二分法穷举以后,我得到
$$ R(x+y=2z^2,2)=93. $$ 下面附上生成 cpf 的python 代码(几年没写过代码)和结果:
|
|

References.
[1] R. Rado, Studien zur Kombinatorik, Math. Z. 36 (1933), 242–280.
[2] S. W. Golomb and L. D. Baumert. “Backtrack programming.” Journal of the ACM (JACM) 12.4 (1965): 516-524.
[3] M. Heule, Schur number five. Thirty-Second AAAI Conference on Artificial Intelligence. 2018.
[4] M. Heule, O. Kullmann, and V. Marek, Solving and verifying the boolean Pythagorean triples problem via cube-and-conquer. International Conference on Theory and Applications of Satisfiability Testing. Springer, Cham, 2016.
[5] M. Nasso and L. Baglini. Ramsey properties of nonlinear Diophantine equations. Advances in Mathematics 324 (2018): 84-117.
[6] B. Green and S. Lindqvist. Monochromatic Solutions to x+y=z2. Canadian Journal of Mathematics 71.3 (2019): 579-605.
