射影虽名为 projective,但并不代表全部意义下的“投影”,而仅仅指的是“点光源的投影”,这也是为什么中文翻译使用“射影”(音同“摄影”)而非“投影”。本文仅从最常见的实射影平面来解释射影平面的几个不太直观或者令人困惑的点。
实射影平面是 $R^3$ 中所有过原点的直线构成的空间,记为 $\mathbb R P^2$ 或简记为 $P^2$。这一定义并不会给我们一个足够清晰的图像,作为“平面”,我们自然会考虑如何定义这一“平面”上的点和线等等。因此我们常常可以根据等价类来具体化。
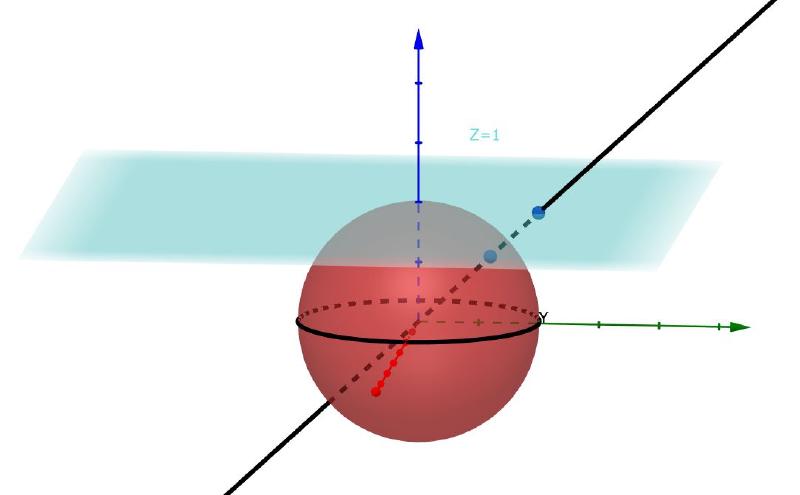
过原点的全部直线可以分为两类,一类是与 xy 平面 (z=0) 有非零倾角的;另一类是位于 xy 平面上的。我们可以任取一个在 $R^3$ 中与 xy 平面平行但不重合的平面,比如 z=1 平面,则前一类的所有直线均在这一平面上有且仅有一个交点。不能选择 xy 平面作为投影平面是因为所有交点会退化为原点。另外一类在 xy 平面上的过原点的直线,并不会与 z=1 平面相交。但是在射影平面中,为了统一这些直线,可以将它们与 z=1 平面的交点定在“无穷远”。无穷远的讲法源自于过原点直线的倾角趋近于0的极限。
因此,我们常常会使用 $R^3\setminus 0$ 的等价类的形式定义。其中两个点 $$ p_1=(x_1,y_1,z_1), \quad p_2=(x_2,y_2,z_2) $$ 等价当且仅当存在非零实数 $\lambda$ 使得 $p_1=\lambda p_2$。因此,我们可以把每个点(等价类)写成一个齐次坐标 $[x:y:z]$ 的形式 (为了方便,我们也可以继续简写为 (x,y,z))。
利用齐次坐标,我们可以将点进行分类。如果一个点的第三坐标 $z\neq 0$ 时,我们可以将齐次坐标写为 (x/z,y/z,1),此时这个点落在平面 z=1 上。如果这个点第三坐标 $z=0$,则此时这个点位于 $xy$-平面中,如果进一步地 $y\neq 0$,则齐次坐标可写为 (x/y,1,0),此时它位于一条直线上;最后如果 $y=z=0$,则齐次坐标为 (1,0,0) (此时 $x\neq 0$)。
事实上,因为射影平面不能无自交地嵌入三维欧几里得空间,因此在三维欧几里得空间中,我们并不能完美的表现射影平面。这里的完美是指既不能把直线“掰弯”,也不能引入“无穷远点”等不直观的概念。射影平面可以嵌入到四维欧几里得空间,这与克莱因瓶类似。
因为无穷远点的关系,上述等价类的定义并没有给我们带来直观上的简单。一个更好的直观化的做法是使用球面(想要直观,只能掰弯)。考虑球面 $x^2+y^2+z^2=1$,则所有过原点的直线均和这一球面有且有 2 个交点。剔除对跖点,我们则可以得到射影空间一一对应的投影点。因此,我们需要完全平分这个球面。
最简单的方法是取“上半球”。但是这牵涉到边界归属的问题,我们还需要平分边界:位于 $xy$-平面上的 $x^2+y^2=1$ 这个圆。继续平分这个圆弧,我们可以取 $y>0$ 的半圆。最后剩下的两个对跖点我们也只取一个 (1,0,0)。如此我们便完成了球面的完全平分,并把射影平面上的点和半球面上的点一一对应。这一方法是把无穷远点收回到 $xy$-平面上的半大圆弧,使其处理起来更加直观。
通过上面的讨论,我们已经感受到使用球面来讨论射影平面是最为直观的。最后我们根据这一理解考虑如下的几个问题:
- 为什么射影平面中的点和直线都是使用一个非零三维向量来表示?(对偶关系)
- 为什么一个点 $m$ 位于一条线 $l$ 当且仅当 $l^Tm=0$ ?
- 为什么平行线的相交于无穷远点?
射影平面上的点在球面投影(绝对平分的上半球面)中是球面上的一点,可以用三维坐标表示,因此任意一点其实也表示一个方向(该点在球面的法向)。
因为直线的定义是最短路径(的延申),而在球面上大圆弧是最短路径。因此射影平面上的直线在球面投影是一个“半大圆”。实际上,任意一个半大圆是半球面和平面 ax+by+cz=0 的交集。我们可以用唯一需要确定的这个平面的法向坐标来定义直线的齐次坐标,即 (a,b,c)。这个三维齐次坐标唯一确定了一条射影平面的直线以及球面的半大圆。特别地,当 a=b=0,这定义了一个无穷远直线。
直线齐次坐标的定义也回答了第二个问题,因为直线上的一点必然满足直线的方程,因此对于直线 l 和它上的点 m,它们的齐次坐标满足 $a x_m +b y_m+c z_m=0$ 亦即 $l^T m=0$。 这也进一步地解释了射影空间的点和直线的对偶关系。更进一步地,一条穿过两点 $m_1, m_2$ 的直线 l 可以用他们的向量积 $m_1\times m_2$ 表示。实际上,过两点的大圆弧(射影直线以及其对应的三维空间的平面)由这两点的向量坐标所确定。两点的向量积给出了它们所在大圆弧(所在平面)的法向量,而这个法向量就是过这两点的(平面表示的)直线 l 的齐次坐标。
第三个问题的直观理解是球面上的平行线类似于地球经线,它们相交于两极,而两极是对跖点,因而只相交于一个无穷远点。因此射影平面的一个重要性质是,任何两条直线相交于一点。
参考文献
- Wikipedia, Real projective plane.
- Wikipedia, Projective plane.
- Marc Pollefeys, The projective plane, Visual 3D Modeling from Images, Tutorial Notes.
whzecomjm 2020-01-09 13:10